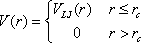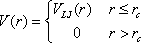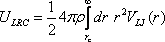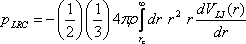Benchmark results for Lennard-Jones fluid

This website is best viewed with younger browsers (for example: Netscape 7, IE 6, Opera 7, Firefox 1)

The information presented here has been organized into six different pages. It is available as web pages or as a single excel file.

1. MD: NVE Molecular dynamics results at liquid-like densities along an isotherm of reduced temperature 0.85. Mean values and standard deviations of temperature, energy, pressure, and diffusion coefficient are reported.
2. MC: NVT Monte Carlo results at both liquid- and vapor-like densities along two isotherms of reduced temperature 0.85 and 0.90. Mean values and standard deviations of energy and pressure are reported.
3. SAT-TMMC: Liquid-vapor coexistence properties obtained by grand-canonical transition-matrix Monte Carlo and histogram re-weighting [1] over the reduced temperature range 0.70 to 1.20 at increments of 0.05. Mean values and standard deviations of the saturation pressure and coexisting liquid and vapor densities, energies, and activities are reported.
4. EOS-TMMC: Equations of state (pressure as a function density) generated by grand-canonical transition-matrix Monte Carlo over the temperature range 0.70 to 1.20 and 1.35 - 1.50 at increments of 0.05. For a given density, the mean pressure and its standard deviation are reported. CPU timings and downloadable raw simulation data (particle number probability distributions) are provided here.
   
5. SAT-EOS: Liquid-vapor coexistence properties as determined from an empirical fit of a large amount of simulation data [2]. The data serve as an approximate guide for liquid-vapor coexistence properties at temperatures other than those investigated in Item 3. Furthermore, the empirical fit should not be used in the vicinity of the critical point.
6. SURFACE TENSION: Surface tension of the Lennard-Jones fluid at various temperatures calculated using explicit molecular dynamics of the liquid-vapor interface and the combination of finite-size scaling and grand-canonical transition-matrix Monte Carlo. The influence of truncation is also investigated in this section.
7. SAT-TMMC: Liquid-vapor coexistence properties for the Lennard-Jones fluid, linear-force shifted at r=2.5σ obtained by grand-canonical transition-matrix Monte Carlo and histogram re-weighting [1] over the reduced temperature range 0.65 to 0.90 at increments of 0.05. Mean values and standard deviations of the saturation pressure and coexisting liquid and vapor densities, energies, and activities are reported.
8. VAPOR-EOS-TMMC: Vapor-phase properties for the Lennard-Jones fluid, linear-force shifted at r=2.5σ obtained by grand-canonical transition-matrix Monte Carlo and histogram re-weighting [1] over the reduced temperature range 0.65 to 0.90 at increments of 0.05. Mean values and standard deviations of the saturation pressure and coexisting liquid and vapor densities, energies, and activities are reported.

As is usually the case, temperature, density (number density), pressure, etc., are given in reduced units (denoted by *). That is, these properties are expressed in terms of the characteristic energy, ε, and length scale, σ, defined by the Lennard-Jones potential:

Therefore, the reduced temperature T*, density ρ*, and pressure p* are k_BT/ε, ρσ³, pσ³/ε, respectively. The critical parameters for the pure LJ fluid have been determined to be T_c* = 1.3120(7), ρ_c* = 0.316(1), and p_c* = 0.1279(6) [3].

For computational expediency, the potential and force are usually truncated at some cutoff distance r_c. That is, the effective potential V(r) is

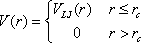
In this work, the cutoff distance is taken to be 3σ, unless noted otherwise. An approximate correction for this truncation to the energy and pressure of the system can be obtained by assuming the spatial correlations beyond the cutoff distance are unity. The reader is referred to Refs. [4] and [5] for these so-called “standard long range corrections” (sLRC). It should be noted that this not a good assumption in inhomogeneous fluids. For completeness, the working expressions for obtaining the long range corrections to the potential energy per particle and virial pressure are provided below:

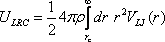
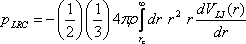
where ρ is the bulk number density, V_LJ(r) is the Lennard-Jones potential energy, and r_c is the truncation (cutoff) distance. A subtle point to note is that the above pressure correction does not account for impulsiive effects at r_c where the potential energy (and therefore the force) changes discontinuously. This is particularly important when trying to simulate directly interfacacial phenomena [6]. Finally, it should be mentioned that other truncation and long range correction schemes for dealing with non-bonded interactions exist [4-8]. In some cases, the truncation schemes can yield critical properties that differ from those quoted above [8].

In future versions, coordinate sets will be available for which the potential energy per particle and the virial are specified. This information can be used to test energy/force routines.

References