Lennard-Jones fluid simulation website

7. SAT-TMMC: Liquid-vapor coexistence properties - Linear-Force Shifted Potential

Liquid-vapor coexistence properties obtained by grand-canonical transition-matrix Monte Carlo and histogram re-weighting over the reduced temperature range 0.65 to 0.90 at increments of 0.05. Mean values of the saturation pressure, density, potential energy per molecule, and activity (chemical potential- see below) for each phase are reported.

METHOD: Grand-canonical transition-matrix Monte Carlo [1] and histogram re-weighting
V/σ3: 512
TRUNCATION: Linear Force Shifted at 2.5σ
Prob. of Disp. Move: 0.40
Prob, of Ins/Del. Move: 0.60
Biasing Function Update Frequency
 1.0E6 trials
Simulation Length: 8.0E9 trials

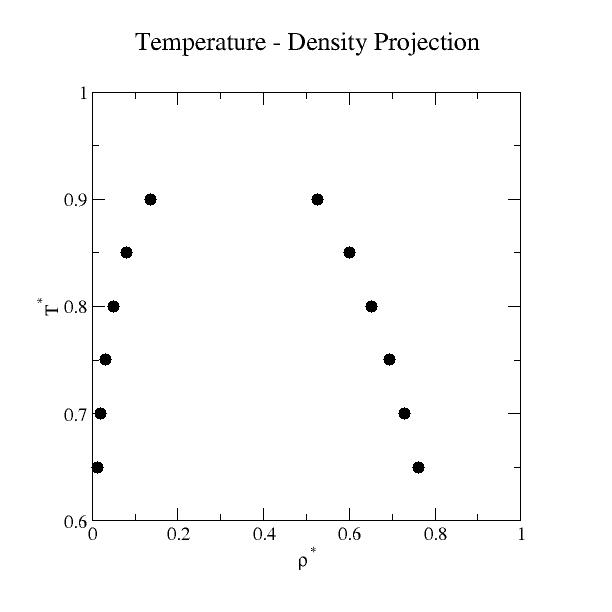
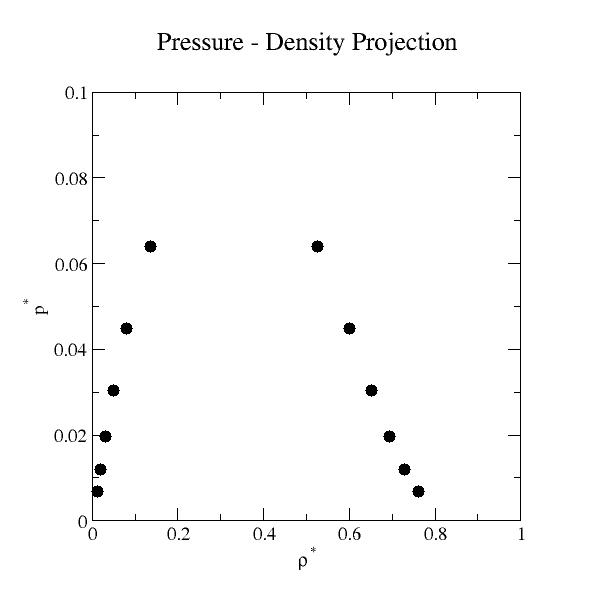
Liquid-Vapor Phase Coexistence Properties:
  
T* ρvap*
 +/- ρliq* +/- psat* +/- Uvap* +/- Uliq* +/- ln z*sat +/-
0.65 1.13086E-02 2.38587E-06 7.61685E-01 1.75209E-04 6.71314E-03 1.28036E-06 -1.11676E-01 2.44461E-05 -4.21546E+00 1.80378E-03 -4.65535E+00 1.74181E-04
0.70 1.95113E-02 1.67304E-06 7.29309E-01 1.93161E-04 1.18969E-02 8.67525E-07 -1.80182E-01 1.61809E-05 -3.99813E+00 4.68222E-04 -4.19453E+00 6.35176E-05
0.75 3.18771E-02 4.34360E-06 6.93338E-01 8.77657E-05 1.95383E-02 2.06799E-06 -2.77685E-01 3.98990E-05 -3.76690E+00 7.03921E-04 -3.81176E+00 8.64963E-05
0.80 5.04378E-02 1.23324E-05 6.52056E-01 1.51115E-04 3.02550E-02 4.98952E-06 -4.16314E-01 1.07693E-04 -3.51491E+00 7.52792E-04 -3.49051E+00 1.23641E-04
0.85 7.95146E-02 1.37074E-05 6.01040E-01 1.36261E-04 4.47490E-02 4.00928E-06 -6.23068E-01 1.14899E-04 -3.22499E+00 6.42761E-04 -3.21839E+00 5.93251E-05
0.90 1.34982E-01 3.46267E-05 5.24430E-01 2.05138E-04 6.39805E-02 4.35001E-06 -1.00685E+00 2.75183E-04 -2.84264E+00 9.86622E-04 -2.98636E+00 3.58074E-05



Remarks:

Uncertainties were obtained from 5 independent simulations and represent 95% confidence limits based on a standard t statistic. Liquid-vapor coexistence was determined by adjusting the activity such that the pressures of the liquid and vapor phases were equal. Here, the pressure is not the conventional virial pressure [2, 3] but is the actual thermodynamic pressure, based on the fact that the absolute free energies can be obtained from the distributions determined from simulation [4]. Alternative methods, for example Gibbs-ensemble Monte Carlo and combination grand-canonical Monte Carlo and histogram re-weighting, can be used to determine liquid-vapor coexistence. A review of standard methods of phase equilibria simulations can be found in Ref. 5.

As introduced in Refs. 2 and 3, the activity, z, is defined as

z = Λ-3 exp(βμ)

where Λ is the de Broglie wavelength, β = 1/(kBT) (where kB is Boltzmann's constant), and μ is the chemical potential. It is sometimes more convenient to work with ln z in the simulations and in post-processing. (NOTE: The reported activity is dimensionless, having been scaled by the LJ length cubed.)

Phase-coexistence energies were obtained by determining the mean potential energy at a given value of N for an additional 8 billion MC trials. Combining this information with the particle number probability distribution, the mean potential energy of the coexisting phases can be calculated [6].

For the Lennard-Jones fluid, linear force shifted at 2.5σ, the critical properties are Tc*=0.937, ρc*=0.320, and pc*=0.0820 [7].

[1] J. R. Errington, J. Chem. Phys. 118, 9915 (2003).
[2] M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids (Oxford University Press, New York, 1989).
[3] D. Frenkel and B. Smit, Understanding Molecular Simulation, 2nd ed. (Academic, San Diego, 2002).
[4] J. R. Errington and A. Z. Panagiotopoulos, J. Chem. Phys. 109, 1093 (1998).
[5] A. Z. Panagiotopoulos, J. Phys.: Condens. Matter 12, 25 (2000).
[6] J. R. Errington and V. K. Shen, J. Chem. Phys. 123, 164103 (2005).
[7] J. R. Errington P. G. Debenedetti, and S. Torquato, J. Chem. Phys. 118, 2256 (2003).